Размеры космоса из античных астрономических источников
| Измерение | Автор | Результат | Факт | Ошибка | Метод |
|---|---|---|---|---|---|
| окружность Земли | Аристотель | 400.000 ст. или 70.000 км | 40.000 км | 2x | неизвестен |
| расстояние до Луны | Аполлоний | 5.000.000 ст. или 960.000 км | 3.500 км | 3.5x | по Дж. Норту |
| окружность Земли | Эратосфен | 250.000 ст. или 45.000 км | 40.000 км | 12% | зенитное расстояние солнца в полдень летнего солнцестояния |
| отношение расстояний | Аристарх | 1/20 | 1/400 | 20x | лунная четверть |
| диаметр Солнца | Аристарх | ~7 R♁ или 90.000 км | 1.400.000 км | 15x | затмение луны |
| диаметр Луны | Аристарх | 20 R☉ или 5.000 км | 3.500 км | 1.5x | затмение луны |
| расстояние до Луны | Аристарх | 10 R♁ или 150.000 км | 390.000 км | 2x | затмение луны; интерпретация данных Аристарха |
| расстояние до Солнца | Аристарх | 20 L☾ или 3.000.000 км | 150.000.000 км | 50x | затмение луны; интерпретация данных Аристарха |
| окружность Земли | Посидоний | 240.000 ст. или 43.000 км | 40.000 км | 8% | верхняя кульминация Канопуса |
| расстояние до Солнца | Посидоний | 10.000 R♁ или 70.000.000 км | 150.000.000 км | 2x | оценка «от балды», 10.000 — греческое «тьма», неопределенно много |
| диаметр Солнца | Посидоний | 3.000.000 ст. или 540.000 км | 1.400.000 км | 2x | отсутствие тени гномона |
| диаметр Луны | Клеомед | ½ ♁ или 40.000 ст. или 7.000 км | 3.500 км | 2x | продолжительность лунного затмения |
| расстояние до Луны | Клеомед | 5.000.000 ст. или 900.000 км | 390.000 км | 2x | продолжительность лунного затмения |
| диаметр Солнца | Клеомед | 520.000 ст. или 93.000 км | 1.400.000 км | 15x | «оценка снизу» по физической скорости орбитального движения |
| расстояние до Солнца | Клеомед | 65.000.000 ст. или 12.000.000 км | 150.000.000 км | 15x | «оценка снизу», согласованная с диаметром |
| диаметр Луны | Клеомед | 40.000 ст. или 7.000 км | 3.500 км | 2x | топографический параллакс луны при солнечном затмении; предложен метод без расчетов |
| диаметр Венеры | Клеомед | 1/6 ☉ | 1/30 ☉ (вид.) | 5x | визуальная оценка |
Размеры Земли
Первое упоминание о размерах Земли обнаруживается у Аристотеля. В книге «О небе» он пишет Математики, пытающиеся вычислить длину земной окружности, называют цифру около 400.000 стадиев
. Возможно, он без ссылок на источник пользуется египетскими или вавилонскими данными, и каким способом получено это значение неизвестно. Стадии в древнем мире были разные, от 157 до 210 метров; примем здесь для оценки стадий в 180 метров, хотя дискуссии о том, какой стадий применяли те или иные авторы, активно ведутся. Используя значение стадия 180 метров, определим длину окружности Земли по анонимным «математикам» Аристотеля около 70.000 км.
Сильно завышено и неизвестно как получено.
Размеры Земли определяли Эратосфен (III в. до н.э.) и Посидоний (II в. до н.э.). Хотя их способы геодезически эквивалентны, но в них использовались разные астрономические явления. Проводили ли они сами реальные наблюдения, о которых говорят, неизвестно.
Эратосфен
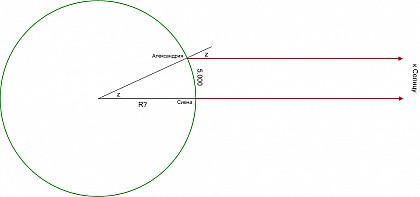
Эратосфен использовал следующий способ. Сиена (нынешний Асуан) и Александрия лежат на одном меридиане и расстояние между ними 5.000 стадий, при этом Сиена лежит на тропике Рака: в день летнего солнцестояния в полдень солнце точно в зените, так как его видно из колодца. Измеряя в этот день полуденную высоту солнца над горизонтом в Александрии (Эратосфен предлагал использовать скафис — солнечные часы специального типа) можно определить длину окружности Земли. Работает этот способ при условии отсутствии топографического параллакса Солнца, что Эратосфен оговаривает и что вообще является общим местом античных авторов.
По Эратосфену длина окружности Земли 250.000 стадий или, по нашему условному стадию в 180 метров, 45.000 км.
Хотя методологически способ Эратосфена выглядит безупречно, Эратосфену довольно повезло, что он так точно оценил размер Земли, его поджидало много погрешностей на пути, которые удачно скомпенсировали друг друга. Расстояние, измеряемое временем движения караванов, не могло быть точным, измерение зенитного расстояния полуденного солнца с помощью колодца тоже не внушает доверия. Да уж кстати говоря, Сиена находится чуть севернее тропика.
Посидоний
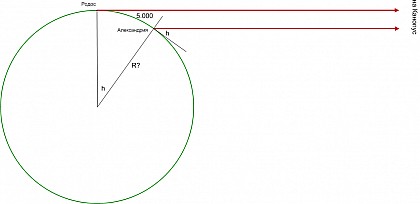
Посидоний основывает расчеты на другом астрономическом наблюдении: верхняя кульминация звезды Канопус ровно на горизонте на острове Родос (ее видно только при наблюдении с горы, но не с равнины), а в Александрии ее высота в кульминации 1/4 знака (этот факт упоминается, например, и Плинием Старшим). Поскольку Александрия южнее Родоса на 5.000 стадий, длина окружности Земли 240.000 стадий, или 43.000 км.
Метод Посидония и его результаты приведены Клеомедом, но у других авторов встречаются и отличающиеся данные Посидония; их я пока опускаю.
Клеомед (ок. I в н.э.) проводит расчет размеров Луны и Солнца и расстояний до них.
Расстояние и размер Луны
Аристарх Самосский
Первый, кто попытался определить расстояние до небесных светил, Луны и Солнца, был Аристарх Самосский в III веке до н.э. Он это сделал в единственной его дошедшей до нас работе «О величинах и расстояниях Солнца и Луны».
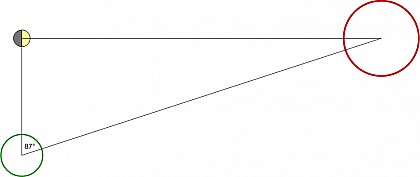
Сначала он находит отношение расстояний до Луны и Солнца, исходя их того, что в момент четверти фазы (первой или последней четверти луны) видимый угол между луной и солнцем 87°. Это отношение он определяет как
1/18 < L☾/L☉ < 1/20
Аристарх сильно ошибся, поскольку фактически указанный угол составляет только 89° 50', так что искомое отношение — 1/400. Нужно сказать, что астрономы того времени просто не имели инструментов, необходимых для точного определения момента четверти фазы. Увы, это была ошибка, обусловленная технологиями, и тут нет ничьей вины.
Но это только отношение расстояний. На пути к значениям самих расстояний Аристарх приводит следующие утверждения:
- (во время лунного затмения) ширина земной тени вмещает две луны;
- видимый диаметр луны 2°.
К этим двум пунктам и схеме также есть замечания. Во-первых, луна «укладывается» в тень не 2, а 2 2/3 раза (это небольшой грех), а во-вторых, видимый диаметр луны не 2°, а в четыре раза меньше, полградуса, ½°. Неясно, откуда взялась такая грубая и досадная ошибка, тем более, что именно Аристарху Самосскому приписывается (Архимедом) определение правильной величины — ½°. Это может быть раннее значение, которое Аристарх потом существенно поправил, или описка самого Аристарха, которую он не заметил в дальнейших вычислениях, или ошибка переписчика, но тогда непонятно, почему ей не противоречит дальнейший текст. Так или иначе, у Аристарха видимый диаметр луны 2°, и мы будем использовать это значение.
На основании заявленных фактов, геометрии затмения и вычисленного ранее отношения расстояний Аристарх определяет, что отношение размеров Солнца и Земли
19/3 < R☉/R♁ < 43/6,
а для Луны, соответственно, в 20 раз меньше. В привычной нам форме и округляя: Солнце больше Земли в 7 раз, Луна меньше в 3 раза. Если использовать оценку Эратосфена (сам Аристарх этого не делает), можно получить диаметр Солнца 90.000 км и диаметр Луны 5.000 км.
Зная физический размер Луны и ее видимый размер (2°), можно было бы вычислить и расстояние до Луны: примерно 10 диаметров Земли. Аристарх этого не делает. Если бы сделал, исходя из оценки Эратосфена у него получилось бы 150.000 км. Соответственно, расстояние до Солнца в 20 раз больше: 3.000.000 км.
Математика Аристарха Самосского
Необходимо отметить, что Аристарх пользуется очень изощренной геометрией в своих построениях. Не смотря на то, что он описывает их в кратких словесных формулировках, он учитывает и конусообразность лунной тени, и тот факт, что освещенная Солнцем часть Луны больше половины шара. Подробный разбор построений Аристарха Самосского и «перевод» на современный математический язык сделан И.Н. Веселовским в статье «Аристарх Самосский — Коперник античного мира» Историко-астрономические исследования, Вып.VII, 1961.
К слову сказать, в этой работе Аристарх Самосский использует тригонометрические мотивы и, в частности, формулирует собственную теорему
tg(α) / tg(β) < α / β < sin(α) / sin(β), при α < β.
Подведем итоги, сравнив результаты Аристарха Самосского с современными.
- отношение расстояний до Луны и Солнца — 1/19, в два раза завышено,
- диаметр Луны в 1.5 раза завышен,
- диаметр Солнца недооценен в 15 раз,
- расстояние до Солнца недооценено в 50 раз,
- расстояние до Луны недооценено в 2 раза.
Клеомед, лунное затмение
Клеомед, как и Аристарх Самосский, использует затмение луны, чтобы определить размер этого светила. Его вариант гораздо проще. Он не использует все те астрономические и геометрические тонкости, которые есть у Аристарха (в частности, считает земную тень цилиндром). Возможно просто потому, что его работа — просто учебник общей астрономии.
Клеомед, так же как и Аристарх, принимает из наблюдений лунных затмений, что диаметр Луны вдвое меньше диаметра Земли или 40.000 стадий. Это примерно 7.000 км вместо 3.500 км, то есть вдвое завышено. Во-первых, луна «укладывается» в тень не 2 раза, а 2 2/3, по-вторых, тень Земли не цилиндр, как расчетах, а конус.
Клеомед, солнечное затмение
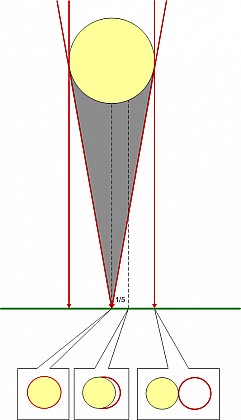
Другой метод расчета размера Луны, предлагаемый Клеомедом, основан на солнечном затмении. В Геллеспонте (пролив Дарданеллы) наблюдалось центральное солнечное затмение, в Александрии центры солнца и луны при затмении были смещены на 1/5 диаметра. Клеомед не проводит расчета, но можно получить диаметр Луны, используя его метод и принимая расстояние между точками наблюдений 7.000 стадий, как у географов того времени. Результат будет около 40.000 стадий, такой же, как и первым способом.
Здесь накопилось несколько измерительных и методологических ошибок. Во-первых, визуальная оценка фазы затмения затруднительна, во-вторых, расстояние между Геллеспонтом и Александрией скорее 5.500 стадий и, наконец, метод работает точно, если полоса затмения перпендикулярна большому кругу, соединяющему точки наблюдений.
Из размера Луны 40.000 стадий Клеомед получает и расстояние до Луны: 5.000.000 стадий или 900.000 км (фактически 390.000 км). Здесь ошибка еще возросла: Клеомед считает, что диаметр луны составляет 1/750 от полной окружности 360°, на самом же деле луна покрупнее — 31' составляет 1/700 от полной окружности. Клеомед объясняет, что величина 1/750 определена путем измерения времени восхода луны над горизонтом с помощью клепсидры. Вероятно, точность такого измерения недостаточна.
Расстояние и размер Солнца
Клеомед
Клеомед также дает оценку для Солнца, исходя из предположения, что все планеты, в частности, Солнце и Луна, движутся с равной линейной скоростью. Принимая равенство видимых диаметров луны и солнца, учитывая длительность года и месяца, он получает ключевое отношение 1/13 и выводит диаметр Солнца 520.000 стадий (93.000 км) и расстояние до Солнца 65.000.000 стадий (12.000.000 км) вместо 1.400.000 и 150.000.000 км соответственно.
Таким образом, параметры Луны Клеомед вдвое завысил, а размер и расстояние до Солнца недооценил на порядок. Он, правда, признает, что это оценка «снизу», поскольку легковерно будет считать, что планеты в своих замысловатых движениях являются равноскоростными
и говорит о своих оценках Солнца: меньшим его не считал никто из физиков и астрономов
.
Посидоний
Оценку размера Солнца предлагал и Посидоний примерно за век до Клеомеда (мы его уже упоминали в самом начале, описывая размеры Земли).
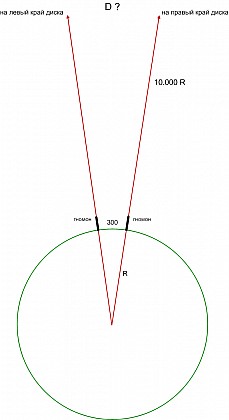
По наблюдением в Сиене (Асуане), лежащем на тропике Рака, в полдень равноденствия гномон не дает тени на полосе шириной 300 стадий, значит какая-то точка диска солнца в зените. Принимая оценку расстояния до Солнца в 10.000 раз больше радиуса Земли, Посидоний получил диаметр Солнца 3.000.000 стадий или 540.000 км (фактически 1.400.000).
10.000
10.000 — греческая мириада, по употреблению схожая нашей «тысячей»: «10.000» — это просто «неопределенно много», a «в 10.000 раз» — «несравнимо много»; эквивалентно употреблявшемуся греками выражению «Земля является точкой в сравнении со сферой Солнца».
Конечно, использование гномона для таких углов кажется самонадеянным. Кстати, здесь же имеем априорную оценку расстояния до Солнца 70.000.000 км.
Посидоний ошибся всего в два раза в определении размеров Солнца и расстояния до него, но это конечно, чисто случайное совпадение.
Расстояние и размеры планет и звезд
Клеомед пытается оценить и физический размер звезд, точнее, планеты Венеры, полагая ее видимый размер 1/6 солнца. Это сильно завышенная оценка, фактически должно быть 1/30. Это оценка «сверху»: сфера Венеры имеет меньший размер, чем сфера Солнца, так что фактический размер Венеры по Клеомеду пропорционально меньше.
Клеомед не приводит числовых расчетов, понимая шаткость оснований, но заверяет, что звезды, в частности неподвижные звезды на внешней сфере, «сфере звезд», значительно более удаленной, чем сфера Венеры, сравнимы по размерам с Солнцем или даже превосходят его.
Арат о планетах
Где и когда их найти, невозможно по прочим светилам
Предугадать — переменчивы всех пяти положенья.
Клеомед, «Учение о круговращении небесных тел»
-
если бы мы взглянули на Землю с высоты (расстояния) Солнца, она в целом показалась бы нам звездой, имеющей самую незначительную величину
, аот сферы неподвижных звезд ее не будет видно
. Само же Солнце, если наблюдать его с высоты (расстояния) неподвижных звёзд, будет иметь звёздную величину
. Это эквивалентно тому, что звезды сравнимы по яркости с Солнцем.